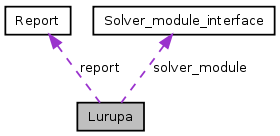
Lurupa Class Reference

Lurupa's core. More...

#include <lurupa/Lurupa.h>

Collaboration diagram for Lurupa:

List of all members.

Public Member Functions

void cond (Lp *lp, double &lower, double &upper)

Compute verified condition number.

Bound_status dual_certificate (Lp *lp)

Compute certificate for primal infeasibility.

const char * get_core_version () const

Get core version string.

char * get_lp_name () const

Get linear program's name.

bool is_lp_maximize () const

Return whether linear program is maximized.

Bound_status lower_bound (Lp *lp, double &bound, int &iterations)

Compute lower bound.

Lurupa ()

Constructor.

Bound_status primal_certificate (Lp *lp)

Compute certificate for dual infeasibility.

void print_core_brief_version () const

Print brief core information.

void print_core_version () const

Print core information.

void print_module_brief_version () const

Print brief module information.

void print_module_version () const

Print module information.

void rho_d (Lp *lp, double &lower, double &upper)

Compute distance to dual infeasibility.

void rho_p (Lp *lp, double &lower, double &upper)

Compute distance to primal infeasibility.

Bound_status upper_bound (Lp *lp, double &bound, int &iterations)

Compute upper bound.

~Lurupa ()

Destructor.

double get_alpha () const

Get algorithm parameter alpha.

double get_eta () const

Get algorithm parameter eta.

bool is_inflate () const

Is inflation set.

void set_alpha (double alpha)

Set algorithm parameter alpha.

void set_eta (double eta)

Set algorithm parameter eta.

void set_inflate (bool inflate)

Set inflation.

const char * get_module_version () const

Get solver module version.

double get_solver_eps () const

Get solver's accuracy.

void lp2solver (Lp *lp)

Set linear program from Lurupa.

void print_module_options () const

Print options supported by module.

Lp * read_lp (FILE *in, const double &relative_interval_radius)

Read linear program.

void set_interface (Solver_module_interface module)

Set solver module.

bool set_lp (Lp *lp, const double relative_interval_radius)

Set linear program from solver.

bool set_module (char *module_path)

Set solver module.

bool set_module_options (Lp *lp, int argc, char *argv[])

Set solver options.

bool set_solution (Lp *lp, void *p)

Set linear program's solution.

Solver_status solve_lp (Lp *lp, double &optimal_value)

Solve linear program.

Public Attributes

Report report

Reporting and debugging.

Private Member Functions

void restore_dual_phase1 (Lp *lp, const INTERVAL_VECTOR &iaT, const INTERVAL_VECTOR &ibT, const VECTOR &xlT, const VECTOR &xuT, const int non_fixed_varsT, const int free_variables_sizeT)

Restore lp after dual phase 1 approach.

void restore_primal_phase1 (Lp *lp, const INTERVAL_VECTOR &icT, const bool maxmimize)

Restore lp after primal phase 1 approach.

void set_dual_phase1 (Lp *lp)

Set dual phase 1 lp.

void set_primal_phase1 (Lp *lp, bool *maximize)

Set primal phase 1 lp.

Find basis

Functions to find basis
These functions are used to find a regular submatrix to rigorously verify the primal or dual constraints.

void add_column_to_basis (int step, INTERVAL_MATRIX &A, INTERVAL_MATRIX &IBasis, int *basis_indices)

Add column to basis.

void do_pivot (MATRIX &LU, int pivot_index, int step, int *basis_indices)

Do the pivot.

void eliminate (MATRIX &LU, int step)

Perform an elimination step.

bool find_basis (INTERVAL_MATRIX &A, int *&basis_indices, int size_basis_indices, INTERVAL_MATRIX &IBasis, MATRIX &Basis_mid_inverse)

Find basis for linear system.

double pivot_element (MATRIX LU, int step, int &pivot_index)

Find pivot element.

void shorten_basis_indices (int *&basis_indices, int basis_size)

Shorten basis indices array.

Lower bound

Compute minimizing lower bound
These functions are used to compute a lower bound for the minimal objective value.

void compute_dual_deflation (Lp *lp, VECTOR &d_c)

Compute dual deflation parameters.

Bound_status compute_lower (Lp *lp, double &bound)

Compute minimizing lower bound.

void decrease_dual_deflation (Lp *lp, VECTOR &d_c)

Decrease dual deflation parameters.

bool find_constraint_basis (Lp *lp, INTERVAL_MATRIX &IResidual, int *&basis_indices, INTERVAL_MATRIX &IBasis, MATRIX &Basis_mid_inverse)

Find constraint basis.

void increase_dual_deflation (Lp *lp, VECTOR &d_c, const INTERVAL_VECTOR &id_pos, const INTERVAL_VECTOR &id_neg)

Increase dual deflation parameters.

void process_initial_dual_solution (Lp *lp, Bound_status &status, double &bound, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int *basis_indices)

Process initial dual solution.

void process_perturbed_dual_solution (Lp *lp, Bound_status &status, double &bound, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int *basis_indices, VECTOR &deflation_c)

Process perturbed dual solution.

Upper bound

Compute minimizing upper bound
These functions are used to compute an upper bound for the minimal objective value.

void compute_primal_deflation (Lp *lp, Primal_deflation &d)

Compute primal deflation parameters.

Bound_status compute_upper (Lp *lp, double &bound)

Compute minimizing upper bound.

void decrease_primal_deflation (Lp *lp, Primal_deflation &d)

Decrease primal deflation parameters.

bool find_equation_basis (Lp *lp, INTERVAL_MATRIX &IResidual, int *&basis_indices, INTERVAL_MATRIX &IBasis, MATRIX &Basis_mid_inverse)

Find equation basis.

void increase_primal_deflation (Lp *lp, Primal_deflation &d)

Increase primal deflation parameters.

void process_initial_primal_solution (Lp *lp, Bound_status &status, double &bound, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int *basis_indices)

Process initial primal solution.

void process_perturbed_primal_solution (Lp *lp, Bound_status &status, double &bound, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int *basis_indices, Primal_deflation &deflation)

Process perturbed primal solution.

Dual feasibility

Establish dual feasibility
These functions are used to establish a dual feasible solution starting from an approximate one delivered by the solver.

Bound_status establish_dual_feasibility (Lp *lp, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int *basis_indices, INTERVAL_VECTOR &id_pos, INTERVAL_VECTOR &id_neg)

Establish dual feasibility.

void establish_iy_simple_bounds (Lp *lp)

Establish simple bounds on lp.iy.

Bound_status establish_lagrange_parameters (Lp *lp, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int *basis_indices, INTERVAL_VECTOR &id_pos, INTERVAL_VECTOR &id_neg)

Establish lagrange parameteres.

Bound_status process_bounded_variables (Lp *lp, INTERVAL_VECTOR &id_pos, INTERVAL_VECTOR &id_neg)

Process bounded variables.

Bound_status process_free_variables (Lp *lp, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int *basis_indices)

Process free variables.

Primal feasibility

Establish primal feasibility
These functions are used to establish a primal feasible solution starting from an approximate one delivered by the solver.

bool establish_equality_constraints (Lp *lp, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int *basis_indices)

Establish equality constraints.

void establish_ix_simple_bounds (Lp *lp)

Establish simple bounds on lp.ix.

Bound_status establish_primal_feasibility (Lp *lp, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int *basis_indices)

Establish primal feasibility.

bool primal_feasible (Lp *lp)

Check for primal feasibility.

Private Attributes

double alpha

Algorithm parameter.

double eps

Algorithm parameter.

double eta

Algorithm parameter.

bool inflate

Try inflation to compute bound.

int iteration

Current iteration count.

int max_iterations

Upper limit for iterations.

lt_dlhandle mod_handle

Handle to solver module object.

Solver_module_interface solver_module

Interface to solver module.

Friends

class Condition

class Lp

Detailed Description

Lurupa's core.

This class implements Lurupa's core logic. It implements the interface visible to the user as well as the algorithm logic to compute the verified bounds using the interface to the solver modules.

Member Function Documentation

void Lurupa::add_column_to_basis	(	int	step,
		INTERVAL_MATRIX &	A,
		INTERVAL_MATRIX &	IBasis,
		int *	basis_indices
	)			`[private]`

Add column to basis.

Set column #step of IBasis to the column of A designated by basis index #step. Zero out the column in A.

Parameters:

`[in]`	step	index into `IBasis` and `basis_indices`
`[in,out]`	A	contains the column to add / zero out
`[out]`	IBasis	receives the basis column
`[in]`	basis_indices	indices of basis columns

Referenced by find_basis().

void Lurupa::compute_dual_deflation	(	Lp *	lp,
		VECTOR &	d_c
	)			`[private]`

Compute dual deflation parameters.

Compute the initial dual deflation parameters for lp.

Parameters:

`[in]`	lp	the LP
`[out]`	d_c	stores the dual deflation paramters

References alpha, eps, eta, Report::get_write_vm(), Lp::IA, Lp::IB, Lp::ic, Lp::infinite, Lp::iy, Lp::iz, Lp::name, report, Report::write_vector(), Lp::xl, and Lp::xu.

Referenced by compute_lower().

Bound_status Lurupa::compute_lower	(	Lp *	lp,
		double &	bound
	)			`[private]`

Compute minimizing lower bound.

Compute the lower bound for the objective function of a minimizing problem. Try iteratively to transform the approximate dual solutions of perturbed problems into intervals verified to contain dual feasible points of the original problem.

Parameters:

`[in]`	lp	the LP
`[out]`	bound	the computed bound

Returns:: status of the bound computation

References bs_rank, bs_running, compute_dual_deflation(), eta, Lp::feasibility, find_constraint_basis(), Lp::ic, iteration, Report::print(), process_initial_dual_solution(), process_perturbed_dual_solution(), report, Solver_module_interface::restore_dual, Solver_module_interface::solve_dual_perturbed, solver_module, ss_feasible, and ss_infeasible.

Referenced by lower_bound(), and upper_bound().

void Lurupa::compute_primal_deflation	(	Lp *	lp,
		Primal_deflation &	d
	)			`[private]`

Compute primal deflation parameters.

Compute the initial primal deflation parameters for lp.

Parameters:

`[in]`	lp	the LP
`[out]`	d	stores the primal deflation paramters

References Primal_deflation::a, alpha, eps, eta, Report::get_write_vm(), Lp::IA, Lp::ia, Lp::infinite, Lp::ix, Lp::name, report, Report::write_vector(), Lp::xl, Primal_deflation::xl, Lp::xu, and Primal_deflation::xu.

Referenced by compute_upper().

Bound_status Lurupa::compute_upper	(	Lp *	lp,
		double &	bound
	)			`[private]`

Compute minimizing upper bound.

Compute the upper bound for the objective function of a minimizing problem. Try iteratively to transform the approximate primal solutions of perturbed problems into intervals verified to contain primal feasible points of the original problem.

Parameters:

`[in,out]`	lp	the LP
`[out]`	bound	the computed bound

Returns:: status of the bound computation

References bs_rank, bs_running, compute_primal_deflation(), eta, Lp::feasibility, find_equation_basis(), iteration, Report::print(), process_initial_primal_solution(), process_perturbed_primal_solution(), report, Solver_module_interface::restore_primal, Solver_module_interface::solve_primal_perturbed, solver_module, ss_feasible, and ss_unbounded.

Referenced by lower_bound(), and upper_bound().

void Lurupa::cond	(	Lp *	lp,
		double &	lower,
		double &	upper
	)

Compute verified condition number.

Compute an enclosure of the condition number of lp.

Parameters:

`[in]`	lp	the LP
`[out]`	lower	lower bound on the condition number
`[out]`	upper	upper bound on the condition number

References Condition::cond(), Report::print(), and report.

Referenced by main().

void Lurupa::decrease_dual_deflation	(	Lp *	lp,
		VECTOR &	d_c
	)			`[private]`

Decrease dual deflation parameters.

Decrease the dual deflation parameters of all constraints. Take the current value into account.

Parameters:

`[in]`	lp	the LP
`[in,out]`	d_c	the dual deflation parameters

References alpha, eta, Report::get_write_vm(), iteration, Lp::name, Report::print(), report, and Report::write_vector().

Referenced by process_perturbed_dual_solution().

void Lurupa::decrease_primal_deflation	(	Lp *	lp,
		Primal_deflation &	d
	)			`[private]`

Decrease primal deflation parameters.

Decrease the primal deflation parameters of all constraints. Take the current value into account.

Parameters:

`[in]`	lp	the LP
`[in,out]`	d	the primal deflation parameters

References Primal_deflation::a, alpha, eta, Report::get_write_vm(), iteration, Lp::name, Report::print(), report, Report::write_vector(), Primal_deflation::xl, and Primal_deflation::xu.

Referenced by process_perturbed_primal_solution().

void Lurupa::do_pivot	(	MATRIX &	LU,
		int	pivot_index,
		int	step,
		int *	basis_indices
	)			`[private]`

Do the pivot.

Swap the columns of LU with indices pivot_index and step and the corresponding entries in basis_indices.

Parameters:

`[in,out]`	LU	matrix to perform pivot on
`[in]`	pivot_index	index of pivot column
`[in]`	step	index of current column
`[in,out]`	basis_indices	indices of basis columns

Referenced by find_basis().

Bound_status Lurupa::dual_certificate ( Lp * lp )

Compute certificate for primal infeasibility.

Try to compute a dual certificate verifying primal infeasibility. A dual certificate comes with a dual improving ray, which is a solution to the homogeneous dual LP with a positive objective value (for a minimizing primal LP). Two approaches are tried.

If the approximate solver offers a mean to extract an approximate dual improving ray, we try to verify a feasible point of the homogeneous dual from it.
If that fails or the solver does not support it, a phase 1 approach is tried. We compute a lower bound for the primal phase 1 problem. If this is positive primal infeasibility is verified and the dual improving ray is derived from the dual enclosure.

Parameters:

[in] lp the LP

Return values:

	bs_priminf	if infeasibility is verified
	bs_failure	otherwise

References bs_failure, bs_priminf, bs_verified, establish_dual_feasibility(), find_constraint_basis(), Solver_module_interface::get_dual_ray, Report::get_level(), Report::get_write_vm(), Lp::ia, Lp::ib, Lp::ic, Lp::infinite, iteration, Lp::ix, Lp::iy, Lp::iz, lower_bound(), Lp::maximize, Lp::name, Report::print(), report, restore_primal_phase1(), set_primal_phase1(), Solver_module_interface::set_primal_phase1, solve_lp(), solver_module, ss_infeasible, Report::write_vector(), Lp::xl, and Lp::xu.

Referenced by compute_dual().

void Lurupa::eliminate	(	MATRIX &	LU,
		int	step
	)			`[private]`

Perform an elimination step.

Perform an elimination step of the LU decomposition of the transpose of LU.

Parameters:

`[in,out]`	LU	matrix to decompose
`[in]`	step	elimination step number

Referenced by find_basis().

Bound_status Lurupa::establish_dual_feasibility	(	Lp *	lp,
		const INTERVAL_MATRIX &	IBasis,
		const MATRIX &	Basis_mid_inverse,
		const INTERVAL_MATRIX &	IResidual,
		const int *	basis_indices,
		INTERVAL_VECTOR &	id_pos,
		INTERVAL_VECTOR &	id_neg
	)			`[private]`

Establish dual feasibility.

Try to establish a dual feasible solution in two steps.

Establish the dual simple bounds on the lagrange parameters of the primal inequality constraints (establish_iy_simple_bounds).
Compute lagrange parameters for the finite primal simple bounds, establish zero lagrange parameters for the infinite primal simple bounds (establish_lagrange_parameters).

Parameters:

`[in]`	lp	the LP
`[in]`	IBasis	dual constraint basis matrix
`[in]`	Basis_mid_inverse	approximate inverse of (midpoint of) `IBasis`
`[in]`	IResidual	residual of dual constraint matrix
`[in]`	basis_indices	indices of dual constraint matrix basis columns
`[out]`	id_pos	lagrange parameters for finite simple lower bounds
`[out]`	id_neg	lagrange parameters for finite simple upper bounds

Returns:: status of the bound computation

References establish_iy_simple_bounds(), establish_lagrange_parameters(), Report::get_write_vm(), iteration, Lp::iy, Lp::iz, Lp::name, Report::print(), report, and Report::write_vector().

Referenced by dual_certificate(), process_initial_dual_solution(), and process_perturbed_dual_solution().

bool Lurupa::establish_equality_constraints	(	Lp *	lp,
		const INTERVAL_MATRIX &	IBasis,
		const MATRIX &	Basis_mid_inverse,
		const INTERVAL_MATRIX &	IResidual,
		const int *	basis_indices
	)			`[private]`

Establish equality constraints.

Establish the equality constraints on the approximate primal solution lp.ix. Assume the columns of the constraint matrix to be partitioned into two sets. The columns indexed by basis_indices form the regular (interval) matrix IBasis. The matrix IResidual, which is a copy of the constraint matrix with the former columns set to zero, contains the remaining columns.

Use the equivalent form of the equality constraints

$Bx = b \quad \Leftrightarrow \quad IBasis \cdot x_{basis\_indices} = b - IResidual \cdot x.$

Try to compute an enclosure for the solution of the new system, fixing the values of the variables not corresponding to the columns in IBasis. If such an enclosure is found, store the enclosure in lp.ix and return true. Otherwise return false.

Parameters:

`[in]`	lp	the LP
`[in]`	IBasis	equality constraint basis matrix
`[in]`	Basis_mid_inverse	approximate inverse of (midpoint of) `IBasis`
`[in]`	IResidual	residual of equality constraint matrix
`[in]`	basis_indices	indices of basis columns

Return values:

	true	if equality constraints could be established,
	false	otherwise

References Lp::ib, and Lp::ix.

Referenced by establish_primal_feasibility().

void Lurupa::establish_ix_simple_bounds ( Lp * lp ) [private]

Establish simple bounds on lp.ix.

Establish the simple bounds lp.xl and lp.xu on the approximate primal solution lp.ix. Assume the elements of the primal solution are point intervals on input. Set the bound violating elements to the violated bound,

$\begin{gathered} lp.ix_i < lp.xl_i \quad \Rightarrow \quad lp.ix_i := lp.xl_i \\ lp.ix_i > lp.xu_i \quad \Rightarrow \quad lp.ix_i := lp.xu_i \end{gathered}$

References Lp::ix, Lp::xl, and Lp::xu.

Referenced by establish_primal_feasibility().

void Lurupa::establish_iy_simple_bounds ( Lp * lp ) [private]

Establish simple bounds on lp.iy.

Establish the simple upper bound 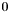$0$ on the approximate dual solution part lp.iy. Assume the elements of the dual solution are point intervals on input. Set the positive elements to zero.

References Lp::iy.

Referenced by establish_dual_feasibility().

Bound_status Lurupa::establish_lagrange_parameters	(	Lp *	lp,
		const INTERVAL_MATRIX &	IBasis,
		const MATRIX &	Basis_mid_inverse,
		const INTERVAL_MATRIX &	IResidual,
		const int *	basis_indices,
		INTERVAL_VECTOR &	id_pos,
		INTERVAL_VECTOR &	id_neg
	)			`[private]`

Establish lagrange parameteres.

Compute lagrange parameters for the primal simple bounds. Check for the computed parameters to be zero for infinite bounds.

Parameters:

`[in]`	lp	the LP
`[in]`	IBasis	dual constraint basis matrix
`[in]`	Basis_mid_inverse	approximate inverse of (midpoint of) `IBasis`
`[in]`	IResidual	residual of dual constraint matrix
`[in]`	basis_indices	indices of dual constraint matrix basis columns
`[out]`	id_pos	lagrange parameters for finite simple lower bounds
`[out]`	id_neg	lagrange parameters for finite simple upper bounds

Returns:: status of the bound computation

References bs_noenc, bs_running, bs_verified, Lp::free_variables_size, process_bounded_variables(), and process_free_variables().

Referenced by establish_dual_feasibility().

Bound_status Lurupa::establish_primal_feasibility	(	Lp *	lp,
		const INTERVAL_MATRIX &	IBasis,
		const MATRIX &	Basis_mid_inverse,
		const INTERVAL_MATRIX &	IResidual,
		const int *	basis_indices
	)			`[private]`

Establish primal feasibility.

Try to establish primal feasibility on the approximate primal solution lp.ix in three steps.

Establish the simple bounds (establish_ix_simple_bounds).
Verify the equality constraints (establish_equality_constraints).
Check if the simple bounds still hold (the approximate solution is changed in step 2) and the inequality constraints are satisfied (primal_feasible).

Parameters:

`[in]`	lp	the LP
`[in]`	IBasis	equality constraint basis matrix
`[in]`	Basis_mid_inverse	approximate inverse of (midpoint of) `IBasis`
`[in]`	IResidual	residual of equality constraint matrix
`[in]`	basis_indices	indices of basis columns

Return values:

	bs_verified	if `lp.ix` is verified to be primal feasible
	bs_noenc	if `lp.ix` violates the equality constraints
	bs_running	if `lp.ix` meets the equality constraints but violates the inequality constraints or simple bounds

References bs_noenc, bs_running, bs_verified, establish_equality_constraints(), establish_ix_simple_bounds(), Report::get_write_vm(), iteration, Lp::ix, Lp::name, primal_feasible(), Report::print(), report, and Report::write_vector().

Referenced by primal_certificate(), process_initial_primal_solution(), and process_perturbed_primal_solution().

bool Lurupa::find_basis	(	INTERVAL_MATRIX &	A,
		int *&	basis_indices,
		int	size_basis_indices,
		INTERVAL_MATRIX &	IBasis,
		MATRIX &	Basis_mid_inverse
	)			`[private]`

Find basis for linear system.

Find a (interval) submatrix of A whose midpoint matrix is regular. Assume that A has more columns than rows. Select linear independent columns from the column candidates indexed by basis_indices. Move the selected columns to the matrix IBasis and zero them out in A. Record the selected columns in the list of candidates.

If a proper (interval) submatrix is found compute its (midpoint's) approximate inverse. Remove the discarded columns from the candidate list and return true. Otherwise return false.

Note:: As A is changed during this method this has to be a copy if it is needed after the call.

Parameters:

`[in,out]`	A	matrix to be processed
`[in,out]`	basis_indices	indices of basis candidates on input, indices of basis columns on output
`[in]`	size_basis_indices	number of basis candidates
`[out]`	IBasis	matrix of basis columns
`[out]`	Basis_mid_inverse	approximate inverse of (midpoint of) `IBasis`

Return values:

	true	if basis could be found,
	false	otherwise

References add_column_to_basis(), do_pivot(), eliminate(), pivot_element(), Report::print(), report, and shorten_basis_indices().

Referenced by find_constraint_basis(), and find_equation_basis().

bool Lurupa::find_constraint_basis	(	Lp *	lp,
		INTERVAL_MATRIX &	IResidual,
		int *&	basis_indices,
		INTERVAL_MATRIX &	IBasis,
		MATRIX &	Basis_mid_inverse
	)			`[private]`

Find constraint basis.

Find a basis of the dual constraints. Select a regular submatrix of the constraint matrix prefering columns corresponding to equality constraints.

Parameters:

`[in]`	lp	the LP
`[in,out]`	IResidual	constraint matrix on input, selected columns set to zero on output
`[out]`	basis_indices	indices of selected columns
`[out]`	IBasis	matrix of selected columns
`[out]`	Basis_mid_inverse	approximate inverse of (midpoint of) `IBasis`

Return values:

	true	if basis could be computed,
	false	otherwise

References find_basis(), Lp::free_variables, Lp::free_variables_size, Lp::IA, Lp::IB, Report::print(), and report.

Referenced by compute_lower(), and dual_certificate().

bool Lurupa::find_equation_basis	(	Lp *	lp,
		INTERVAL_MATRIX &	IResidual,
		int *&	basis_indices,
		INTERVAL_MATRIX &	IBasis,
		MATRIX &	Basis_mid_inverse
	)			`[private]`

Find equation basis.

Find a basis of the equality constraints. Select a regular submatrix of the constraint matrix using only columns corresponding to non-fixed variables, that is variables with different lower and upper simple bound.

Parameters:

`[in]`	lp	the LP
`[in,out]`	IResidual	constraint matrix on input, selected columns set to zero on output
`[out]`	basis_indices	indices of selected columns
`[out]`	IBasis	matrix of selected columns
`[out]`	Basis_mid_inverse	approximate inverse of (midpoint of) `IBasis`

Return values:

	true	if basis could be computed
	false	otherwise

References find_basis(), Lp::IB, Lp::non_fixed_vars, Report::print(), report, Lp::xl, and Lp::xu.

Referenced by compute_upper(), and primal_certificate().

double Lurupa::get_alpha ( ) const

Get algorithm parameter alpha.

Get the agorithm parameter alpha.

References alpha.

Referenced by clu_get_alpha().

const char * Lurupa::get_core_version ( ) const

Get core version string.

Get the core version string.

References version.

Referenced by clu_get_core_version().

double Lurupa::get_eta ( ) const

Get algorithm parameter eta.

Get the algorithm parameter eta.

References eta.

Referenced by clu_get_eta().

const char * Lurupa::get_module_version ( ) const

Get solver module version.

Get the solver module version string

References Solver_module_interface::get_version, mod_handle, Report::print(), report, and solver_module.

Referenced by clu_get_module_version().

double Lurupa::get_solver_eps ( ) const

Get solver's accuracy.

Get solver accuracy epsilon.

References eps, mod_handle, Report::print(), and report.

Referenced by clu_get_solver_eps().

void Lurupa::increase_dual_deflation	(	Lp *	lp,
		VECTOR &	d_c,
		const INTERVAL_VECTOR &	id_pos,
		const INTERVAL_VECTOR &	id_neg
	)			`[private]`

Increase dual deflation parameters.

Increase the dual deflation parameters of the violated constraints. Take the current value into account.

Parameters:

`[in]`	lp	the LP
`[in,out]`	d_c	the deflation parameters
`[in]`	id_pos	lagrange parameter of simple lower bound
`[in]`	id_neg	lagrange parameter of simple upper bound

References alpha, eta, Report::get_write_vm(), Lp::infinite, iteration, Lp::ix, Lp::name, Report::print(), report, Report::write_vector(), Lp::xl, and Lp::xu.

Referenced by process_perturbed_dual_solution().

void Lurupa::increase_primal_deflation	(	Lp *	lp,
		Primal_deflation &	d
	)			`[private]`

Increase primal deflation parameters.

Increase the primal deflation parameters of the violated constraints. Take the current value into account.

Parameters:

`[in]`	lp	the LP
`[in,out]`	d	the deflation parameters

References Primal_deflation::a, alpha, eta, Report::get_write_vm(), Lp::IA, Lp::ia, iteration, Lp::ix, Lp::name, Report::print(), report, Report::write_vector(), Primal_deflation::xl, Lp::xl, Primal_deflation::xu, and Lp::xu.

Referenced by process_perturbed_primal_solution().

bool Lurupa::is_inflate ( ) const

Is inflation set.

Get the algorithm flag inflate.

References inflate.

Referenced by clu_is_inflate().

Bound_status Lurupa::lower_bound	(	Lp *	lp,
		double &	bound,
		int &	iterations
	)

Compute lower bound.

Compute the lower bound of the linear program lp by calling compute_lower or compute_upper for the minimizing problem as appropriate. Return a status value indicating that the computation succeeded or why it failed.

Parameters:

`[in,out]`	lp	the LP
`[out]`	bound	computed lower bound
`[out]`	iterations	iterations needed to compute bound

Returns:: the value returned by compute_lower or compute_upper

References compute_lower(), compute_upper(), iteration, and Lp::maximize.

Referenced by clu_lower_bound(), compute_lower(), dual_certificate(), Condition::rho_d(), and Condition::rho_p().

double Lurupa::pivot_element	(	MATRIX	LU,
		int	i,
		int &	j_pivot
	)			`[private]`

Find pivot element.

Find the pivot element, which is the element with largest absolute value in row i of LU and return its value and column index.

Parameters:

`[in]`	LU	matrix to find pivot in
`[in]`	i	row number to search pivot in
`[out]`	j_pivot	column index of pivot element

Returns:: the value of the pivot element

Referenced by find_basis().

Bound_status Lurupa::primal_certificate ( Lp * lp )

Compute certificate for dual infeasibility.

Try to compute a primal certificate verifying dual infeasibility. A primal certificate comes with a primal improving ray, which is a solution to the homogeneous primal LP with a negative objective value (for a minimizing primal LP). Two approaches are tried.

If the approximate solver offers a mean to extract an approximate primal improving ray, we try to verify a feasible point of the homogeneous primal from it.
If that fails or the solver does not support it, a phase 1 approach is tried. We compute an upper bound for the dual phase 1 problem. If this is negative dual infeasibility is verified and the primal improving ray is derived from the primal enclosure.

Parameters:

[in] lp the LP

Return values:

	bs_dualinf	if infeasibility is verified
	bs_failure	otherwise

References bs_dualinf, bs_failure, bs_verified, establish_primal_feasibility(), find_equation_basis(), Lp::free_variables_size, Report::get_level(), Solver_module_interface::get_primal_ray, Report::get_write_vm(), Lp::ia, Lp::ib, Lp::ic, iteration, Lp::ix, Lp::maximize, Lp::name, Lp::non_fixed_vars, Report::print(), report, restore_dual_phase1(), set_dual_phase1(), Solver_module_interface::set_dual_phase1, solve_lp(), solver_module, ss_unbounded, upper_bound(), Report::write_vector(), Lp::xl, and Lp::xu.

Referenced by compute_primal().

bool Lurupa::primal_feasible ( Lp * lp ) [private]

Check for primal feasibility.

Test if the approximate primal solution lp.ix satisfies the inequality constraints. Assuming the approximate solution satisfies the simple bounds and contains points satisfying the equality constraints this means lp.ix contains verified primal feasible points.

Return values:

	true	if approximate solution is primal feasible,
	false	otherwise

References Report::get_level(), Lp::ia, Lp::IA, Lp::ix, Report::print(), report, Lp::xl, and Lp::xu.

Referenced by establish_primal_feasibility().

void Lurupa::print_module_options ( ) const

Print options supported by module.

Print the options supported by solver module.

References mod_handle, Report::print(), Solver_module_interface::print_options, report, and solver_module.

Referenced by clu_print_module_options(), and print_usage().

Bound_status Lurupa::process_bounded_variables	(	Lp *	lp,
		INTERVAL_VECTOR &	id_pos,
		INTERVAL_VECTOR &	id_neg
	)			`[private]`

Process bounded variables.

Compute lagrange parameters for the primal simple bounds of the bounded variables (i.e., variables with at least one finite bound) satisfying the dual constraints. Check for the computed parameters to be zero for infinite simple bounds. Return bs_verified if this is the case, bs_running otherwise.

Parameters:

`[in]`	lp	the LP
`[out]`	id_pos	lagrange parameter for finite simple lower bound
`[out]`	id_neg	lagrange parameter for finite simple upper bound

Return values:

	bs_verified	if the infinite simple bounds' parameters are zero,
	bs_running	otherwise

References bs_running, bs_verified, Report::get_level(), Lp::IA, Lp::IB, Lp::ic, Lp::infinite, Lp::iy, Lp::iz, Report::print(), report, Lp::xl, and Lp::xu.

Referenced by establish_lagrange_parameters().

Bound_status Lurupa::process_free_variables	(	Lp *	lp,
		const INTERVAL_MATRIX &	IBasis,
		const MATRIX &	Basis_mid_inverse,
		const INTERVAL_MATRIX &	IResidual,
		const int *	basis_indices
	)			`[private]`

Process free variables.

Establish zero lagrange parameters for the infinite simple bounds of the free variables. Set the lagrange parameters to zero. Try to find an enclosure of the solution set of the dual constraints corresponding to the free variables. If this fails return bs_noenc, otherwise return bs_running.

Parameters:

`[in]`	lp	the LP
`[in]`	IBasis	dual constraint basis matrix
`[in]`	Basis_mid_inverse	approximate inverse of (midpoint of) `IBasis`
`[in]`	IResidual	residual matrix of dual constraint matrix
`[in]`	basis_indices	indices of dual constraint matrix basis columns

Return values:

	bs_running	if zero lagrange parameters could be established for free variables,
	bs_noenc	otherwise

References bs_noenc, bs_running, Lp::free_variables, Lp::free_variables_size, Lp::ic, Lp::iy, and Lp::iz.

Referenced by establish_lagrange_parameters().

void Lurupa::process_initial_dual_solution	(	Lp *	lp,
		Bound_status &	status,
		double &	bound,
		const INTERVAL_MATRIX &	IBasis,
		const MATRIX &	Basis_mid_inverse,
		const INTERVAL_MATRIX &	IResidual,
		const int *	basis_indices
	)			`[private]`

Process initial dual solution.

Process the approximate dual solution of the original problem. Based on the solver's judgement of the problem's feasibility try to verify a feasible solution, start iterating, or set an infinite bound if no verification is possible.

Parameters:

`[in]`	lp	the LP
`[out]`	status	status of bound computation
`[out]`	bound	rigorous bound
`[in]`	IBasis	dual constraint basis matrix
`[in]`	Basis_mid_inverse	approximate inverse of (midpoint of) `IBasis`
`[in]`	IResidual	residual of dual constraint matrix
`[in]`	basis_indices	indices of dual constraint matrix basis columns

References bs_failure, bs_noenc, bs_orgunb, bs_timeout, bs_verified, establish_dual_feasibility(), Lp::feasibility, Lp::ia, Lp::ib, Lp::infinite, Lp::ix, Lp::iy, Lp::iz, Report::print(), report, ss_failure, ss_feasible, ss_infeasible, ss_timeout, ss_unbounded, Lp::xl, and Lp::xu.

Referenced by compute_lower().

void Lurupa::process_initial_primal_solution	(	Lp *	lp,
		Bound_status &	status,
		double &	bound,
		const INTERVAL_MATRIX &	IBasis,
		const MATRIX &	Basis_mid_inverse,
		const INTERVAL_MATRIX &	IResidual,
		const int *	basis_indices
	)			`[private]`

Process initial primal solution.

Process the approximate primal solution to the original problem. Based on the solver's judgement of the problem's feasibility try to verify a feasible solution, start iterating, or set an infinite bound if no verification is possible.

Parameters:

`[in]`	lp	the LP
`[out]`	status	status of bound computation
`[out]`	bound	rigorous bound
`[in]`	IBasis	equality constraint basis matrix
`[in]`	Basis_mid_inverse	approximate inverse of (midpoint of) `IBasis`
`[in]`	IResidual	residual of equality constraint matrix
`[in]`	basis_indices	indices of equality constraint matrix basis columns

References bs_failure, bs_noenc, bs_orginf, bs_timeout, bs_verified, establish_primal_feasibility(), Lp::feasibility, Lp::ic, Lp::ix, Report::print(), report, ss_failure, ss_feasible, ss_infeasible, ss_timeout, and ss_unbounded.

Referenced by compute_upper().

void Lurupa::process_perturbed_dual_solution	(	Lp *	lp,
		Bound_status &	status,
		double &	bound,
		const INTERVAL_MATRIX &	IBasis,
		const MATRIX &	Basis_mid_inverse,
		const INTERVAL_MATRIX &	IResidual,
		const int *	basis_indices,
		VECTOR &	deflation_c
	)			`[private]`

Process perturbed dual solution.

Process the approximate dual solution to a perturbed problem. Based on the solver's judgement of the problem's feasibility try to verify the feasibility and modify the deflation parameters as appropriate. If the iteration count exceeds the maximum max_iterations set an infinite bound.

Parameters:

`[in]`	lp	the LP
`[out]`	status	status of bound computation
`[out]`	bound	rigorous bound
`[in]`	IBasis	equality constraint basis matrix
`[in]`	Basis_mid_inverse	approximate inverse of (midpoint of) `IBasis`
`[in]`	IResidual	residual of equality constraint matrix
`[in]`	basis_indices	indices of equality constraint matrix basis columns
`[in,out]`	deflation_c	the current deflation parameters on input the new deflation parameters on output

References bs_failure, bs_iter, bs_noenc, bs_pertinf, bs_timeout, bs_verified, decrease_dual_deflation(), establish_dual_feasibility(), Lp::feasibility, Lp::ia, Lp::ib, increase_dual_deflation(), Lp::infinite, inflate, iteration, Lp::ix, Lp::iy, Lp::iz, max_iterations, Report::print(), report, ss_failure, ss_feasible, ss_infeasible, ss_timeout, ss_unbounded, Lp::xl, and Lp::xu.

Referenced by compute_lower().

void Lurupa::process_perturbed_primal_solution	(	Lp *	lp,
		Bound_status &	status,
		double &	bound,
		const INTERVAL_MATRIX &	IBasis,
		const MATRIX &	Basis_mid_inverse,
		const INTERVAL_MATRIX &	IResidual,
		const int *	basis_indices,
		Primal_deflation &	deflation
	)			`[private]`

Process perturbed primal solution.

Process the approximate primal solution to a perturbed problem. Based on the solver's judgement of the problem's feasibility try to verify a feasible solution and modify the deflation parameters as appropriate. If the iteration count exceeds the maximum max_iterations set an infinite bound.

Parameters:

`[in]`	lp	the LP
`[out]`	status	status of bound computation
`[out]`	bound	rigorous bound
`[in]`	IBasis	equality constraint basis matrix
`[in]`	Basis_mid_inverse	approximate inverse of (midpoint of) `IBasis`
`[in]`	IResidual	residual of equality constraint matrix
`[in]`	basis_indices	indices of equality constraint matrix basis columns
`[in,out]`	deflation	the current deflation parameters on input the new deflation parameters on output

References bs_failure, bs_iter, bs_noenc, bs_pertinf, bs_timeout, bs_verified, decrease_primal_deflation(), establish_primal_feasibility(), Lp::feasibility, Lp::ic, increase_primal_deflation(), inflate, iteration, Lp::ix, max_iterations, Report::print(), report, ss_failure, ss_feasible, ss_infeasible, ss_timeout, and ss_unbounded.

Referenced by compute_upper().

Lp * Lurupa::read_lp	(	FILE *	in,
		const double &	relative_interval_radius
	)

Read linear program.

Instruct the solver module to read a linear program.

Parameters:

`[in]`	in	pointer to linear program
`[in]`	relative_interval_radius	interval radius to inflate lp parameters to

Return values:

	true	if file read successfully,
	false	otherwise

References eta, Solver_module_interface::read_lp, Lp::set_lurupa(), and solver_module.

Referenced by clu_read_lp(), and main().

void Lurupa::restore_dual_phase1	(	Lp *	lp,
		const INTERVAL_VECTOR &	iaT,
		const INTERVAL_VECTOR &	ibT,
		const VECTOR &	xlT,
		const VECTOR &	xuT,
		const int	non_fixed_varsT,
		const int	free_variables_sizeT
	)			`[private]`

Restore lp after dual phase 1 approach.

Reverse the changes from set_dual_phase1 and primal_certificate applied to lp.

Parameters:

`[in,out]`	lp	the LP
`[in]`	iaT	backup of the original right hand sides of inequalities
`[in]`	ibT	backup of the original right hand sides of equations
`[in]`	xlT	backup of the original simple lower bounds
`[in]`	xuT	backup of the original simple upper bounds
`[in]`	non_fixed_varsT	backup of original Lp::non_fixed_vars
`[in]`	free_variables_sizeT	backup of original Lp::free_variables_size

References Lp::feasibility, Lp::free_variables_size, Lp::ia, Lp::ib, Lp::non_fixed_vars, Solver_module_interface::restore_dual_phase1, solver_module, ss_unbounded, Lp::xl, and Lp::xu.

Referenced by primal_certificate().

void Lurupa::restore_primal_phase1	(	Lp *	lp,
		const INTERVAL_VECTOR &	icT,
		const bool	maximize
	)			`[private]`

Restore lp after primal phase 1 approach.

Reverse the changes from set_primal_phase1 applied to lp.

Parameters:

`[in,out]`	lp	the LP
`[in]`	icT	backup of the original objective function
`[in]`	maximize	is the original lp maximized.

References Lp::feasibility, Lp::IA, Lp::IB, Lp::ic, Lp::ix, Lp::maximize, Lp::non_fixed_vars, Solver_module_interface::restore_primal_phase1, solver_module, ss_infeasible, Lp::xl, and Lp::xu.

Referenced by dual_certificate().

void Lurupa::rho_d	(	Lp *	lp,
		double &	lower,
		double &	upper
	)

Compute distance to dual infeasibility.

Compute an enclosure of the distance to dual infeasibility 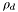$\rho_d$ for lp.

Parameters:

`[in]`	lp	the LP
`[out]`	lower	lower bound on 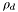$\rho_d$
`[out]`	upper	upper bound on 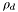$\rho_d$

References Report::print(), report, and Condition::rho_d().

Referenced by main().

void Lurupa::rho_p	(	Lp *	lp,
		double &	lower,
		double &	upper
	)

Compute distance to primal infeasibility.

Compute an enclosure of the distance to primal infeasibility 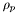$\rho_p$ for lp.

Parameters:

`[in]`	lp	the LP
`[out]`	lower	lower bound on 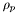$\rho_p$
`[out]`	upper	upper bound on 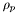$\rho_p$

References Report::print(), report, and Condition::rho_p().

Referenced by main().

void Lurupa::set_alpha ( double alpha )

Set algorithm parameter alpha.

Set the algorithm parameter alpha.

Referenced by clu_set_alpha(), and main().

void Lurupa::set_dual_phase1 ( Lp * lp ) [private]

Set dual phase 1 lp.

Modify lp to be a dual phase 1 problem. Add slacks to the dual constraints that may be violated and put just these with negative coefficients into the objective (positive ones when minimizing the dual). For the primal this procedure boils down to

setting all infinite simple bounds to (for example) 1 and all finite ones to 0
making all constraints homogeneous.

This allows nonzero lagrange parameters for all simple bounds and removes all terms in the dual objective that do not correspond to originally infinite simple bounds.

$\begin{alignedat}{2} \textbf{Before} \\ \min& &\quad&c^Tx \\ \text{subject to}&&&Ax \leq a\\ &&&Bx = b\\ &&&\underline{x} \leq x \leq \overline{x} \\ \\ \\ \\ \end{alignedat} \qquad \longrightarrow \qquad \begin{alignedat}{2} \textbf{After} \\ \min& &\quad&0 \\ \text{subject to}&&&Ax \leq 0\\ &&&Bx = 0\\ &&&x \geq \begin{cases} -1 &\text{if } \underline{x} = -\infty\\ 0 &\text{otherwise} \end{cases} \\ &&&x \leq \begin{cases} 1 &\text{if } \overline{x} = \infty\\ 0 &\text{otherwise} \end{cases} \end{alignedat}$

The objective vector 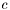$c$ was at this point already cleared by primal_certificate.

Parameters:

[in,out] lp the LP

References Lp::free_variables_size, Lp::infinite, Lp::ix, Lp::non_fixed_vars, Solver_module_interface::set_dual_phase1, solver_module, Lp::xl, and Lp::xu.

Referenced by primal_certificate().

void Lurupa::set_eta ( double eta )

Set algorithm parameter eta.

Set the algorithm parameter eta.

Referenced by clu_set_eta(), and main().

void Lurupa::set_inflate ( bool inflate )

Set inflation.

Set the algorithm flag inflate.

Referenced by clu_set_inflate(), and main().

void Lurupa::set_interface ( Solver_module_interface module )

Set solver module.

Directly set the already initialized interface to a solver module.

Parameters:

[in] module the module interface

References eps, Solver_module_interface::get_accuracy, Solver_module_interface::init, report, and solver_module.

Referenced by clu_set_interface().

bool Lurupa::set_lp	(	Lp *	lp,
		const double	relative_interval_radius
	)

Set linear program from solver.

Use the solver module to transform the linear program lp.

Parameters:

`[in]`	lp	the linear program
`[in]`	relative_interval_radius	interval radius to inflate lp parameters to

Return values:

	true	if the linear program is transformed successfully,
	false	otherwise

References eta, Solver_module_interface::set_lp, and solver_module.

Referenced by clu_set_lp().

bool Lurupa::set_module ( char * module_path )

Set solver module.

Open the solver module pointed to by module_path using the ltdl API. Set up the interface to the solver module by initializing the function pointers in solver_module and get solver specific parameters.

Parameters:

[in] module_path path to solver module

Return values:

	true	if the module could be opened,
	false	otherwise

References eps, Solver_module_interface::get_accuracy, get_func_pointers(), Solver_module_interface::init, mod_handle, report, and solver_module.

Referenced by clu_set_module(), and main().

bool Lurupa::set_module_options	(	Lp *	lp,
		int	argc,
		char *	argv[]
	)

Set solver options.

Pass the solver options to the solver module.

Parameters:

`[in,out]`	lp	the LP
`[in]`	argc	count of solver options
`[in]`	argv	array of solver option strings

Return values:

	true	if options set successfully,
	false	otherwise

References Report::print(), report, Solver_module_interface::set_module_options, and solver_module.

Referenced by clu_set_module_options(), and main().

void Lurupa::set_primal_phase1	(	Lp *	lp,
		bool *	maximize
	)			`[private]`

Set primal phase 1 lp.

Modify lp to be a primal phase 1 problem. Add bounded slacks for all constraints and minimize the slack sum.

$\begin{alignedat}{2} \textbf{Before} \\ \min& &\quad&c^Tx \\ \text{subject to}&&&Ax \leq a\\ &&&Bx = b\\ &&&\underline{x} \leq x \leq \overline{x} \\ \\ \end{alignedat} \qquad \longrightarrow \qquad \begin{alignedat}{2} \textbf{After} \\ \min& &\quad&1^Ts + 1^Tt^+ + 1^Tt^- \\ \text{subject to}&&&Ax - s\leq a\\ &&&Bx + t^+ - t^-= b\\ &&&\underline{x} \leq x \leq \overline{x} \\ &&& 0 \leq s \leq \overline{s}, \; 0 \leq t^+ \leq \overline{t}^+, \; 0 \leq t^- \leq \overline{t}^- \end{alignedat}$

The upper bounds on the slacks are chosen in a way that 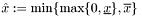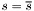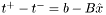$\hat{x} := \min\{\max\{0, \underline{x}\}, \overline{x}\}$ , $s = \overline{s}$ , $t^+ - t^- = b - B\hat{x}$ is feasible.

Parameters:

`[in,out]`	lp	the LP
`[out]`	maximize	is `lp` maximized

References Lp::ia, Lp::IA, Lp::ib, Lp::IB, Lp::ic, Lp::infinite, Lp::ix, Lp::maximize, Lp::non_fixed_vars, Solver_module_interface::set_primal_phase1, solver_module, Lp::xl, and Lp::xu.

Referenced by dual_certificate().

void Lurupa::shorten_basis_indices	(	int *&	basis_indices,
		int	basis_size
	)			`[private]`

Shorten basis indices array.

Shorten the basis_indices array to the first basis_size elements.

Parameters:

`[in,out]`	basis_indices	array to shorten
`[in]`	basis_size	size to achieve

Referenced by find_basis().

Solver_status Lurupa::solve_lp	(	Lp *	lp,
		double &	optimal_value
	)

Solve linear program.

Instruct the solver module to approximately solve lp.

Parameters:

`[in]`	lp	the LP
`[out]`	optimal_value	the approximate optimal value computed by the solver

Returns:: the status of the solver

References Lp::feasibility, Solver_module_interface::solve_original, and solver_module.

Referenced by clu_solve_lp(), dual_certificate(), main(), primal_certificate(), Condition::rho_d(), and Condition::rho_p().

Bound_status Lurupa::upper_bound	(	Lp *	lp,
		double &	bound,
		int &	iterations
	)

Compute upper bound.

Compute the upper bound of a linear program by calling compute_lower or compute_upper for the minimizing problem as appropriate. Return a status value indicating that the computation succeeded or why it failed.

Parameters:

`[in,out]`	lp	the LP
`[out]`	bound	computed upper bound
`[out]`	iterations	iterations needed to compute bound

Returns:: the value returned by compute_lower or compute_upper

References compute_lower(), compute_upper(), iteration, and Lp::maximize.

Referenced by clu_upper_bound(), compute_upper(), primal_certificate(), Condition::rho_d(), and Condition::rho_p().

The documentation for this class was generated from the following files:


Public Member Functions
void	cond (Lp *lp, double &lower, double &upper)
	Compute verified condition number.
Bound_status	dual_certificate (Lp *lp)
	Compute certificate for primal infeasibility.
const char *	get_core_version () const
	Get core version string.
char *	get_lp_name () const
	Get linear program's name.
bool	is_lp_maximize () const
	Return whether linear program is maximized.
Bound_status	lower_bound (Lp *lp, double &bound, int &iterations)
	Compute lower bound.
	Lurupa ()
	Constructor.
Bound_status	primal_certificate (Lp *lp)
	Compute certificate for dual infeasibility.
void	print_core_brief_version () const
	Print brief core information.
void	print_core_version () const
	Print core information.
void	print_module_brief_version () const
	Print brief module information.
void	print_module_version () const
	Print module information.
void	rho_d (Lp *lp, double &lower, double &upper)
	Compute distance to dual infeasibility.
void	rho_p (Lp *lp, double &lower, double &upper)
	Compute distance to primal infeasibility.
Bound_status	upper_bound (Lp *lp, double &bound, int &iterations)
	Compute upper bound.
	~Lurupa ()
	Destructor.

double	get_alpha () const
	Get algorithm parameter alpha.
double	get_eta () const
	Get algorithm parameter eta.
bool	is_inflate () const
	Is inflation set.
void	set_alpha (double alpha)
	Set algorithm parameter alpha.
void	set_eta (double eta)
	Set algorithm parameter eta.
void	set_inflate (bool inflate)
	Set inflation.

const char *	get_module_version () const
	Get solver module version.
double	get_solver_eps () const
	Get solver's accuracy.
void	lp2solver (Lp *lp)
	Set linear program from Lurupa.
void	print_module_options () const
	Print options supported by module.
Lp *	read_lp (FILE *in, const double &relative_interval_radius)
	Read linear program.
void	set_interface (Solver_module_interface module)
	Set solver module.
bool	set_lp (Lp *lp, const double relative_interval_radius)
	Set linear program from solver.
bool	set_module (char *module_path)
	Set solver module.
bool	set_module_options (Lp lp, int argc, char argv[])
	Set solver options.
bool	set_solution (Lp lp, void p)
	Set linear program's solution.
Solver_status	solve_lp (Lp *lp, double &optimal_value)
	Solve linear program.
Public Attributes
Report	report
	Reporting and debugging.
Private Member Functions
void	restore_dual_phase1 (Lp *lp, const INTERVAL_VECTOR &iaT, const INTERVAL_VECTOR &ibT, const VECTOR &xlT, const VECTOR &xuT, const int non_fixed_varsT, const int free_variables_sizeT)
	Restore lp after dual phase 1 approach.
void	restore_primal_phase1 (Lp *lp, const INTERVAL_VECTOR &icT, const bool maxmimize)
	Restore lp after primal phase 1 approach.
void	set_dual_phase1 (Lp *lp)
	Set dual phase 1 lp.
void	set_primal_phase1 (Lp lp, bool maximize)
	Set primal phase 1 lp.
Find basis
Functions to find basis These functions are used to find a regular submatrix to rigorously verify the primal or dual constraints.
void	add_column_to_basis (int step, INTERVAL_MATRIX &A, INTERVAL_MATRIX &IBasis, int *basis_indices)
	Add column to basis.
void	do_pivot (MATRIX &LU, int pivot_index, int step, int *basis_indices)
	Do the pivot.
void	eliminate (MATRIX &LU, int step)
	Perform an elimination step.
bool	find_basis (INTERVAL_MATRIX &A, int *&basis_indices, int size_basis_indices, INTERVAL_MATRIX &IBasis, MATRIX &Basis_mid_inverse)
	Find basis for linear system.
double	pivot_element (MATRIX LU, int step, int &pivot_index)
	Find pivot element.
void	shorten_basis_indices (int *&basis_indices, int basis_size)
	Shorten basis indices array.
Lower bound
Compute minimizing lower bound These functions are used to compute a lower bound for the minimal objective value.
void	compute_dual_deflation (Lp *lp, VECTOR &d_c)
	Compute dual deflation parameters.
Bound_status	compute_lower (Lp *lp, double &bound)
	Compute minimizing lower bound.
void	decrease_dual_deflation (Lp *lp, VECTOR &d_c)
	Decrease dual deflation parameters.
bool	find_constraint_basis (Lp lp, INTERVAL_MATRIX &IResidual, int &basis_indices, INTERVAL_MATRIX &IBasis, MATRIX &Basis_mid_inverse)
	Find constraint basis.
void	increase_dual_deflation (Lp *lp, VECTOR &d_c, const INTERVAL_VECTOR &id_pos, const INTERVAL_VECTOR &id_neg)
	Increase dual deflation parameters.
void	process_initial_dual_solution (Lp lp, Bound_status &status, double &bound, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int basis_indices)
	Process initial dual solution.
void	process_perturbed_dual_solution (Lp lp, Bound_status &status, double &bound, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int basis_indices, VECTOR &deflation_c)
	Process perturbed dual solution.
Upper bound
Compute minimizing upper bound These functions are used to compute an upper bound for the minimal objective value.
void	compute_primal_deflation (Lp *lp, Primal_deflation &d)
	Compute primal deflation parameters.
Bound_status	compute_upper (Lp *lp, double &bound)
	Compute minimizing upper bound.
void	decrease_primal_deflation (Lp *lp, Primal_deflation &d)
	Decrease primal deflation parameters.
bool	find_equation_basis (Lp lp, INTERVAL_MATRIX &IResidual, int &basis_indices, INTERVAL_MATRIX &IBasis, MATRIX &Basis_mid_inverse)
	Find equation basis.
void	increase_primal_deflation (Lp *lp, Primal_deflation &d)
	Increase primal deflation parameters.
void	process_initial_primal_solution (Lp lp, Bound_status &status, double &bound, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int basis_indices)
	Process initial primal solution.
void	process_perturbed_primal_solution (Lp lp, Bound_status &status, double &bound, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int basis_indices, Primal_deflation &deflation)
	Process perturbed primal solution.
Dual feasibility
Establish dual feasibility These functions are used to establish a dual feasible solution starting from an approximate one delivered by the solver.
Bound_status	establish_dual_feasibility (Lp lp, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int basis_indices, INTERVAL_VECTOR &id_pos, INTERVAL_VECTOR &id_neg)
	Establish dual feasibility.
void	establish_iy_simple_bounds (Lp *lp)
	Establish simple bounds on `lp.iy`.
Bound_status	establish_lagrange_parameters (Lp lp, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int basis_indices, INTERVAL_VECTOR &id_pos, INTERVAL_VECTOR &id_neg)
	Establish lagrange parameteres.
Bound_status	process_bounded_variables (Lp *lp, INTERVAL_VECTOR &id_pos, INTERVAL_VECTOR &id_neg)
	Process bounded variables.
Bound_status	process_free_variables (Lp lp, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int basis_indices)
	Process free variables.
Primal feasibility
Establish primal feasibility These functions are used to establish a primal feasible solution starting from an approximate one delivered by the solver.
bool	establish_equality_constraints (Lp lp, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int basis_indices)
	Establish equality constraints.
void	establish_ix_simple_bounds (Lp *lp)
	Establish simple bounds on `lp.ix`.
Bound_status	establish_primal_feasibility (Lp lp, const INTERVAL_MATRIX &IBasis, const MATRIX &Basis_mid_inverse, const INTERVAL_MATRIX &IResidual, const int basis_indices)
	Establish primal feasibility.
bool	primal_feasible (Lp *lp)
	Check for primal feasibility.
Private Attributes
double	alpha
	Algorithm parameter.
double	eps
	Algorithm parameter.
double	eta
	Algorithm parameter.
bool	inflate
	Try inflation to compute bound.
int	iteration
	Current iteration count.
int	max_iterations
	Upper limit for iterations.
lt_dlhandle	mod_handle
	Handle to solver module object.
Solver_module_interface	solver_module
	Interface to solver module.
Friends
class	Condition
class	Lp