DEMOFLBETA A demonstration of flbeta-numbers: precision-p base-beta arithmetic

Initialization
Extreme quantities
Basic operations
Display of flbeta numbers
Vector and matrix operations
Sparse matrices
Other matrix routines
Doubled precision accumulation of dot products
Mixed precisions
Directed rounding
Predecessor and successor
Rounding to nearest
Comparison to IEEE754 single precision
The relative rounding error unit
Checking theorems in precision-p base-beta arithmetic
Interval operations
Interval vectors and matrices
Nice pictures
Enjoy INTLAB

Initialization

Some time ago I published a paper on simulating a lower precision in a given precision. More precisely, if a precision-m base-beta arithmetic is given, then it is shown how to derive a precision-k base-beta arithmetic for k<m. The INTLAB fl-toolbox implements these methods for binary arithmetic [since only binary is available on our computers].

Recently I wrote a paper

S.M. Rump: IEEE-754 precision-$p$ base-$\beta$ arithmetic implemented in binary,
     ACM Transactions on Mathematical Software (ACM TOMS), 49(4), p. 1-21.

how to realize an IEEE 754 conformant precision-p base-beta arithmetic using binary64 (double precision) or uint64 as underlying arithmetic. The precision p is from p=2 until p=64 including the Babylonian base 60 system. The maximal precision p depends on the base:

beta    2   3   5   8  10  16  25  40  60  64
----------------------------------------------
max p  32  20  13  10   9   8   6   6   5   5

if uint64 is the underlying format, and

beta    2   3   5   8  10  16  25  40  60  64
----------------------------------------------
max p  26  15  10   8   7   6   5   4   4   4

if binary64 is the underlying format.

The purpose of this flbeta-toolbox is to simulate an IEEE 754 conformant arithmetic including over- and underflow, exceptional values, directed rounding and alike. An flbeta interval arithmetic is included as well.

First the precision p, the base beta and exponent range is to be specified.

format compact
setround(0)
p = 4;
beta = 10;
E = 50000;
flbetainit('Uint64Representation')
flbetainit(p,beta,E)

===> Using uint64 for representation
ans =
    'Initialization of flbeta-format to 4 mantissa base-10 digits and exponent range -50000 .. 50000'

The underlying format is specified to be uint64 for a 4-digit decimal arithmetic. The maximal precision depends on the base and is computed by

maximalDecimalPresisionUint64 = precmax(10)

maximalDecimalPresisionUint64 =
     9

The maximal precision reduces for internal binary64 representation:

flbetainit('Binary64Representation')
maximalDecimalPresisionBinary64 = precmax(10)

===> Using binary64 for representation
maximalDecimalPresisionBinary64 =
     7

The exponent range is basically limited by the double precision format and independent of the basis. So huge exponents like 1e15 are possible. An example of an operation which is far outside the double precision overflow range is

x = flbeta(1e100)
x500 = x^500

flbeta-type x =
+1.000 * 10^+00100   
flbeta-type x500 =
+Inf

To retrieve the current setting of precision and exponent range use

flbetainit

flbeta-format set to 4 mantissa base-10 digits with exponent range -50000 .. 50000

Extreme quantities

In binary64 the largest and smallest normalized, and the the smallest denormalized number is computed by

realmax
realmin
subrealmin

ans =
  1.7977e+308
ans =
  2.2251e-308
ans =
  4.9407e-324

Similarly, those quantities for the current flbeta format compute by

realmax('flbeta')
realmin('flbeta')
subrealmin('flbeta')

flbeta-type ans =
+9.999 * 10^+50000   
flbeta-type ans =
+1.000 * 10^-50000   
flbeta-type ans =
+0.001 * 10^-50000

Basic operations

The four basic operations are executed as usual, for example (still in base 3)

x = flbeta(11)
y = flbeta(3)
z = x*y
t = (-sqrt(y) + 1/y)*(1:3)

flbeta-type x =
+1.100 * 10^+00001   
flbeta-type y =
+3.000 * 10^+00000   
flbeta-type z =
+3.300 * 10^+00001   
flbeta-type t =
-1.399 * 10^+00000   -2.798 * 10^+00000   -4.197 * 10^+00000

Note that if one operand is of flbeta type, then the flbeta operation is used. That means that the order of operations may be important although mathematically the result is the same. Consider, in decimal arithmetic:

flbetainit(2,10,99)
X = flbeta(7)
res1 = 42/7*X
res2 = X*42/7

Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults. 
ans =
    'Initialization of flbeta-format to 2 mantissa base-10 digits and exponent range -99 .. 99'
flbeta-type X =
+7.0 * 10^+00    
flbeta-type res1 =
+4.2 * 10^+01    
flbeta-type res2 =
+4.1 * 10^+01

For res1, 42/7 = 6 is computed in double precision, and 6*X = 42 does not cause a rounding error in 2-digit decimal format and is the result res1.

However, for res2 first X*42 = 294 is computed in flbeta arithmetic and rounded into 290; then 290/7 = 41.428... is rounded into res2 = 41 in flbeta arithmetic.

Display of flbeta numbers

A convenient way of displaying flbeta numbers is to use the digits to the current base. So for decimal arithmetic we obtain our usual format:

flbetainit(4,10,99)
x = flbeta(1234)

Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults. 
ans =
    'Initialization of flbeta-format to 4 mantissa base-10 digits and exponent range -99 .. 99'
flbeta-type x =
+1.234 * 10^+03

For other bases that applies similarly:

flbetainit(2,16,99)
y = flbeta(254)

Warning: flbeta-package already initialized with different beta; mixing formats
may produce wrong reaults. 
Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults. 
ans =
    'Initialization of flbeta-format to 2 mantissa base-16 digits and exponent range -99 .. 99'
flbeta-type y =
+F.E * 16^+01

For large basis that might be difficult to read, as for the Babylonian system:

flbetainit('Uint64Representation')
flbetainit(5,60,99)
y = flbeta(123456789)

===> Using uint64 for representation
Warning: flbeta-package already initialized with different beta; mixing formats
may produce wrong reaults. 
Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults. 
ans =
    'Initialization of flbeta-format to 5 mantissa base-60 digits and exponent range -99 .. 99'
flbeta-type y =
+9.VXX9 * 60^+04

Because that is difficult to decipher, the individual digits can be displayed as decimal numbers:

format flbetadigits
y

===> Display flbeta-variables by base-beta digits in decimal
flbeta-type y =
+  9. 31 33 33  9 * 60^+04

The rationale is that sum([9 31 33 33 9].*(60.^(4:-1:0))) = 123456789. Of course, also the double precision value of a flbeta quantity may be displayed:

format flbetadouble
y

===> Display flbeta-variables as doubles
flbeta-type y =
   123456789

Vector and matrix operations

Vector and matrix operations are supported as well, for example

A = flbeta(reshape(1:16,4,4))
B = A + 25
C = A*A

flbeta-type A =
     1     5     9    13
     2     6    10    14
     3     7    11    15
     4     8    12    16
flbeta-type B =
    26    30    34    38
    27    31    35    39
    28    32    36    40
    29    33    37    41
flbeta-type C =
    90   202   314   426
   100   228   356   484
   110   254   398   542
   120   280   440   600

Sparse matrices

Sparse vectors and matrices of flbeta-numbers as well as flbeta-intervals are specified as usual.

n = 4;
A = flbeta(band(circulant(1:n),1,2))
S = sparse(A)
[I,J] = find(S);
IJ = [ I' ; J' ]
is_sp = issparse(S)
nnzS = nnz(S)
[p,q] = bandwidth(S)

flbeta-type A =
     1     2     3     0
     4     1     2     3
     0     4     1     2
     0     0     4     1
flbeta-type S =
   (1,1)        1
   (2,1)        4
   (1,2)        2
   (2,2)        1
   (3,2)        4
   (1,3)        3
   (2,3)        2
   (3,3)        1
   (4,3)        4
   (2,4)        3
   (3,4)        2
   (4,4)        1
IJ =
     1     2     1     2     3     1     2     3     4     2     3     4
     1     1     2     2     2     3     3     3     3     4     4     4
is_sp =
  logical
   1
nnzS =
    12
p =
     1
q =
     2

Other matrix routines

Many of the usual operations for full and sparse matrices are available in precision-p base-beta arithmetic.

t = trace(S)
D = diag(S,-1)

flbeta-type t =
   (1,1)        4
flbeta-type D =
   (1,1)        4
   (2,1)        4
   (3,1)        4

Doubled precision accumulation of dot products

The difference between double precision computations and precision-p base-beta arithmetic can be explored. The default for matrix products is accumulation of dot products in working precision to simulate p-digit precision for all operations. For summation and dot products, doubled precision accumulation is possible.

The following generates some Toeplitz matrix and accumulates a residual first in double precision.

flbetainit(12,2,99)
flbetainit('AccumulateBinary64')
n = 4;
A = toeplitz(1:n)
Ainv = inv(A)
resdble = eye(n) - A*Ainv
resflbeta_64 = eye(n) - flbeta(A)*Ainv

Warning: flbeta-package already initialized with different beta; mixing formats
may produce wrong reaults. 
Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults. 
ans =
    'Initialization of flbeta-format to 12 mantissa base-2 digits and exponent range -99 .. 99'
===> flbeta-accumulation in binary64
A =
     1     2     3     4
     2     1     2     3
     3     2     1     2
     4     3     2     1
Ainv =
   -0.4000    0.5000    0.0000    0.1000
    0.5000   -1.0000    0.5000    0.0000
    0.0000    0.5000   -1.0000    0.5000
    0.1000    0.0000    0.5000   -0.4000
resdble =
   1.0e-15 *
         0   -0.1480   -0.2220   -0.2220
   -0.1665    0.2220   -0.2220         0
   -0.0555    0.0370    0.1110   -0.1110
   -0.1665    0.0740   -0.1665         0
flbeta-type resflbeta_64 =
   1.0e-15 *
         0   -0.1480   -0.2220   -0.2220
   -0.1665         0   -0.2220         0
   -0.0555    0.0370         0   -0.1110
   -0.1665    0.0740   -0.1665         0

Note that using flbeta(eye(n)) in the last statement would not change the result because 1 and 0 is exactly representable in any 12-bit precision.

The same computation with the internal precision accumulation of dot products is as follows:

flbetainit('AccumulateFlbeta')
resfl_12 = eye(n) - flbeta(A)*Ainv

===> flbeta-accumulation in working precision [flbeta]
flbeta-type resfl_12 =
   1.0e-03 *
         0   -0.0000         0         0
         0         0         0         0
    0.1831   -0.0000         0         0
    0.0916   -0.0000         0         0

As may be expected, some components are better, some are worse.

Mixed precisions

Mixed operations between flbeta-numbers and single or double numbers are first executed and then rounded. This is unambiguous if the double number is exactly representable in the specified precision-p base-beta format. However

flbeta(32) < flbeta(33)
flbeta(32) == flbeta(33)
flbeta(32) == 33

ans =
  logical
   1
ans =
  logical
   0
ans =
  logical
   0

Here flbeta(33)=32, so care is necessary when mixing formats.

In general, mixing flbeta quantities defined for different precision and/or format is hazardous, the result is not reliable.

Directed rounding

The flbeta operations respect directed rounding. For example, adding a tiny number in rounding to nearest to a large number cannot change its value:

flbetainit(4,10,1000)
setround(0)
x = 2^100
x1 = x + 1

Warning: flbeta-package already initialized with different beta; mixing formats
may produce wrong reaults. 
Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults. 
ans =
    'Initialization of flbeta-format to 4 mantissa base-10 digits and exponent range -1000 .. 1000'
x =
   1.2677e+30
x1 =
   1.2677e+30

The same is true for flbeta numbers:

y = flbeta(1e100)
y1 = y + 1

flbeta-type y =
  1.0000e+100
flbeta-type y1 =
  1.0000e+100

However, changing the rounding to upwards changes the result:

setround(1)
y1up = y + 1

flbeta-type y1up =
  1.0010e+100

Predecessor and successor

A sequence of consecutive precision-p base-beta flbeta-numbers may be computed by

flbetainit(4,10,99);
x = flbeta(32)
[ pred(x) x succ(x) succ(x,2) ]

flbeta-type x =
   32.0000
flbeta-type ans =
   31.9900   32.0000   32.0100   32.0200

Rounding to nearest

In binary64, mostly the rounding to nearest with roundTiesToEven is adopted. It means, that if an internal result is exactly the midpoint between two adjacent floating-point numbers, then the neighbor with even mantissa is chosen as result.

In the flbeta-toolbox that same rule can be used:

setround(0)
flbetainit(4,10,99)
flbetainit('RoundTiesToEven')
x = flbeta(1234)
y = x - 0.5

ans =
    'Initialization of flbeta-format to 4 mantissa base-10 digits and exponent range -99 .. 99'
===> Rounding to nearest with RoundTiesToEven
flbeta-type x =
        1234
flbeta-type y =
        1234

Recently also the option rounding to nearest with roundTiesToAway found its way into the IEEE 754 standard. That is also possible in the flbeta toolbox:

flbetainit('RoundTiesToAway')
X = flbeta(2345)
Xaway = X - 0.5
flbetainit('RoundTiesToEven')
Xeven = X - 0.5

===> Rounding to nearest with RoundTiesToAway
flbeta-type X =
        2345
flbeta-type Xaway =
        2345
===> Rounding to nearest with RoundTiesToEven
flbeta-type Xeven =
        2344

Comparison to IEEE754 single precision

The following

   prec = 24; beta = 2; Emin = -126; Emax = 127;

specifies the same binary format as binary32 (single precision). That means the result in that flbeta format and computed in single precision should coincide. However, library routines in Matlab may use a different order of computation, for example, for dot products, so that results in single and flbeta-arithmetic may be different. Consider

flbetainit(prec,beta,Emin,Emax);       % same as IEEE754 single precision
x = single(randn(1000,1));             % random single precision vector
noroundingerror = all(x == flbeta(x))  % verifies that x is exactly representable in flbeta
s = x'*x                               % dot product in single precision
t = flbeta(x)'*x                       % dot product in flbeta format
s-t                                    % difference of results

Warning: flbeta-package already initialized with different beta; mixing formats
may produce wrong reaults. 
Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults. 
noroundingerror =
  logical
   1
s =
  single
  1.0740e+03
flbeta-type t =
   1.0740e+03
flbeta-type ans =
   6.1035e-04

The bit pattern of the single precision and flbeta computation is

getbits(s)
format flbetabase
t

ans =
    ' +1.00001100011111110001110 * 2^10'
===> Display flbeta-variables by base-beta representation
flbeta-type t =
+1.00001100011111110001001 * 2^+010

Obviously the results computed in single precision and the flbeta-package do not coincide. This is due to a Matlab library routine to compute the dot product x'*x. Computed in a loop, the result by single precision and the flbeta-package are identical. To verify see

s_loop = single(0);
for i=1:1000                    % dot product x'*x by conventional loop
  s_loop = s_loop + x(i)*x(i);
end
s_loop - s                      % difference to Matlab library routine
s_loop - t                      % difference to flbeta-package

ans =
  single
 -6.1035e-04
flbeta-type ans =
+0.00000000000000000000000

The relative rounding error unit

Mathematically, the relative rounding error unit for precision-p base beta arithmetic is 0.5*beta(1-p); that is the maximal relative error when rounding a real number into the flbeta-format. However, it is known that just above a power of beta the relative error is larger, and just below it is smaller.

flbetainit(4,16,99);
x = linspace(0,20,10000);
X = flbeta(x);
close
plot(x,relerr(x,X))

Warning: flbeta-package already initialized with different beta; mixing formats
may produce wrong reaults. 
Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults.

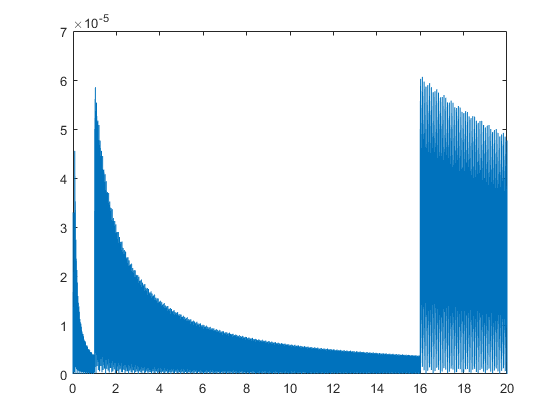
Note the large factor between the best and worst relative error.

At the beginning of the computing age, IBM preferred the hexadecimal basis because of its significantly larger exponent range. However, the change of relative error just below and above a power of 16 came as a price.

That phenomemon is always present, in any basis; here is an example for base 3:

flbetainit(4,3,99);
x = linspace(0,20,10000);
X = flbeta(x);
close
plot(x,relerr(x,X))

Warning: flbeta-package already initialized with different beta; mixing formats
may produce wrong reaults.

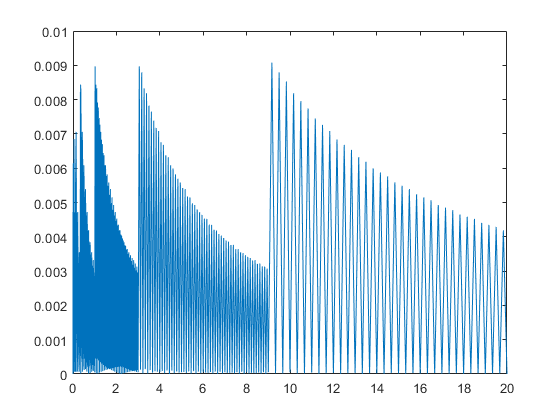
However, the difference between largest and smallest relative error decreases with the basis, the best is for binary arithmetic. Moreover, base 2 offers the advantage of one extra bit (the implicit 1 due to normalization), therefore we use binary arithmetic nowadays.

Checking theorems in precision-p base-beta arithmetic

The flbeta toolbox stores precision-p base-beta as mantissa and exponent separately, i.e., as pair(m,e) such that x = m*beta^e represents the flbeta number. Then 1 <= m < beta^p.

We may want to compute sqrt(x) by first approximating it in double precision and then round it into flbeta format. Rewrite x as x = M * beta^(2E) with 1 <= M < beta^(p+1), then sqrt(x) = sqrt(M)*beta^E.

However, is computing sqrt(M) in double precision and then round it into precision-p base-beta format correct, i.e., may a double rounding occur?

To that end, the routine "flbetasequence(a,b)" is useful producing all flbeta numbers in the interval [a,b]. For example, all denormalized 5-bit binary numbers for exponent range -100..100 is produced by

flbetainit(5,2,99)
x = flbetasequence(0,realmin('flbeta'));
denorm = x(2:end-1)

Warning: flbeta-package already initialized with different beta; mixing formats
may produce wrong reaults. 
Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults. 
ans =
    'Initialization of flbeta-format to 5 mantissa base-2 digits and exponent range -99 .. 99'
flbeta-type denorm =
  Columns 1 through 4
+0.0001 * 2^-99         +0.0010 * 2^-99         +0.0011 * 2^-99         +0.0100 * 2^-99         
  Columns 5 through 8
+0.0101 * 2^-99         +0.0110 * 2^-99         +0.0111 * 2^-99         +0.1000 * 2^-99         
  Columns 9 through 12
+0.1001 * 2^-99         +0.1010 * 2^-99         +0.1011 * 2^-99         +0.1100 * 2^-99         
  Columns 13 through 15
+0.1101 * 2^-99         +0.1110 * 2^-99         +0.1111 * 2^-99

The double rounding can be tested by checking all possibilities for M. Consider a 3-decimal digit arithmetic, i.e., p = 3 and beta = 10. The following code checks all possibilities:

p = 3
beta = 10
flbetainit(p,beta,99)
x = flbetasequence(beta^(p-1),beta^(p+1)-1);
xsqrtdouble = sqrt(x);
xsqrtapproxflbeta = flbeta(xsqrtdouble);
xsqrtflbeta = sqrt(flbeta(x));
index = find(xsqrtapproxflbeta~=xsqrtflbeta)

p =
     3
beta =
    10
Warning: flbeta-package already initialized with different beta; mixing formats
may produce wrong reaults. 
Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults. 
ans =
    'Initialization of flbeta-format to 3 mantissa base-10 digits and exponent range -99 .. 99'
index =
  1×0 empty double row vector

The resulting index set is empty, so there is no double rounding using this approach. We may want to go further and check this for all precisions from 1 to 5 and all basis between 2 and 16:

wng = warning;
warning off
for p=1:5
  for beta=2:16
    flbetainit(p,beta,99);
    x = flbetasequence(beta^(p-1),beta^(p+1)-1);
    xsqrtdouble = sqrt(x);
    xsqrtapproxflbeta = flbeta(xsqrtdouble);
    xsqrtflbeta = sqrt(flbeta(x));
    index = find(xsqrtapproxflbeta~=xsqrtflbeta);
    if any(index(:))
      [p beta]
    end
  end
end
warning(wng)

Again, all index sets are empty, so there is no double rounding in all those cases.

Interval operations

Intervals with flbeta-number as endpoints are supported as well. For example,

flbetainit(2,10,99)
x = flbeta(infsup(1,2))
3*x - 1
x/3

Warning: flbeta-package already initialized with different beta; mixing formats
may produce wrong reaults. 
Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults. 
ans =
    'Initialization of flbeta-format to 2 mantissa base-10 digits and exponent range -99 .. 99'
flbeta-type intval x =
 [ +1.0 * 10^+00  , +2.0 * 10^+00  ] 
flbeta-type intval ans =
 [ +2.0 * 10^+00  , +5.0 * 10^+00  ] 
flbeta-type intval ans =
 [ +3.3 * 10^-01  , +6.7 * 10^-01  ]

The syntax and semantic is as for intervals with double precision endpoints, rounding is always outwards.

flbetainit(4,2,99)
z = flbeta(infsup(32,33))
double(z)

Warning: flbeta-package already initialized with different beta; mixing formats
may produce wrong reaults. 
Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults. 
ans =
    'Initialization of flbeta-format to 4 mantissa base-2 digits and exponent range -99 .. 99'
flbeta-type intval z =
 [ +1.000 * 2^+05       , +1.001 * 2^+05       ] 
intval ans = 
[   32.0000,   36.0000]

The integer 33 is not representable in 4 binary bits but rounded into the next flbeta number 100100_2 = 36.

Interval vectors and matrices

Again interval vectors and matrices of flbeta-numbers as well as the operation between those are as usual.

n = 3;
flbetainit(5,10,99)
A = midrad(flbeta(randn(n)),1e-3)
P = A*intval(A')
C = compmat(A)

Warning: flbeta-package already initialized with different beta; mixing formats
may produce wrong reaults. 
Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults. 
ans =
    'Initialization of flbeta-format to 5 mantissa base-10 digits and exponent range -99 .. 99'
flbeta-type intval A =
  Columns 1 through 2
 [ +2.6456 * 10^+00  , +2.6478 * 10^+00  ]  [ -2.0811 * 10^+00  , -2.0789 * 10^+00  ] 
 [ -5.4755 * 10^-02  , -5.2754 * 10^-02  ]  [ -8.0350 * 10^-01  , -8.0149 * 10^-01  ] 
 [ +4.7150 * 10^-01  , +4.7351 * 10^-01  ]  [ -4.5779 * 10^-01  , -4.5578 * 10^-01  ] 
  Column 3
 [ +1.9286 * 10^-01  , +1.9487 * 10^-01  ] 
 [ +8.8853 * 10^-01  , +8.9054 * 10^-01  ] 
 [ -1.5928 * 10^+00  , -1.5906 * 10^+00  ] 
flbeta-type intval P =
  Columns 1 through 2
 [ +1.1357 * 10^+01  , +1.1380 * 10^+01  ]  [ +1.6925 * 10^+00  , +1.7063 * 10^+00  ] 
 [ +1.6925 * 10^+00  , +1.7063 * 10^+00  ]  [ +1.4346 * 10^+00  , +1.4417 * 10^+00  ] 
 [ +1.8845 * 10^+00  , +1.8999 * 10^+00  ]  [ -1.0792 * 10^+00  , -1.0702 * 10^+00  ] 
  Column 3
 [ +1.8845 * 10^+00  , +1.8999 * 10^+00  ] 
 [ -1.0792 * 10^+00  , -1.0702 * 10^+00  ] 
 [ +2.9600 * 10^+00  , +2.9710 * 10^+00  ] 
flbeta-type C =
+2.6456 * 10^+00    -2.0811 * 10^+00    -1.9487 * 10^-01    
-5.4755 * 10^-02    +8.0149 * 10^-01    -8.9054 * 10^-01    
-4.7351 * 10^-01    -4.5779 * 10^-01    +1.5906 * 10^+00

Note that by definition Ostrowski's comparison matrix is a point matrix.

Nice pictures

For some precision-p base-beta format, let an flbeta-number x in that format be given. To produce some picture we might be interested in what is the probability that (k*x)/k is equal to x.

To check we choose, for example, precision prec=2 and base beta=11 and generate the sequence x of all flbeta numbers with exponent 0. Then the following picture is generated.

prec = 2;
beta = 9;
flbetainit(prec,beta,99);
x = flbetasequence(1,pred(flbeta(beta)));
numElmts = length(x)
M = zeros(numElmts);
for k=1:numElmts
  M(k,:) = ( (k*x)/k == x );
end
close
spy(M)

Warning: flbeta-package already initialized with different beta; mixing formats
may produce wrong reaults. 
Warning: flbeta-package already initialized with different beta format; mixing
formats may produce wrong reaults. 
numElmts =
    72

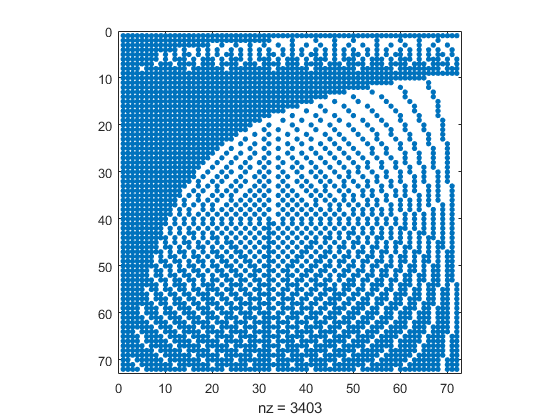
Now we may check the percentage of (k*x)/k producing x again by

p = 100*nnz(M)/numels(M)

p =
   65.6443

So in almost two third of cases, the original x was reproduced.

Enjoy INTLAB

INTLAB was designed and written by S.M. Rump, head of the Institute for Reliable Computing, Hamburg University of Technology. Suggestions are always welcome to rump (at) tuhh.de